ADSTAT
INTERAKTIVNÍ STATISTICKÝ SOFTWARE

ADSTAT 2.0 je interaktivní systém pro statistické zpracování dat. Byl vyvinut na základě dlouholetých zkušeností s numerickými algoritmy pro potřeby výzkumných ústavů, podniků, laboratoří, úřadů a jiných pracovišť, kde se pracuje s experimentálními údaji. Dodává se buď v české nebo anglické verzi. Při zachování velmi přehledné obsluhy nabízí v osmi samostatných modulech téměř třicet různých metod jednorozměrné a vícerozměrné statistické analýzy, lineární a nelineární regrese, diagnostiky dat a modelu, metody pro predikce, analýza rozptylu a řada testů.

OVLÁDÁNÍ

Přes značnou rozsáhlost se ADSTAT velmi snadno ovládá. Jeho obsluha je založena na sytému nabídek, které jsou uživateli nabízeny v logickém sledu. Zadání parametrů, podmínek výpočtu, či jiné akce je vyřešeno systémem panelů, které se objeví vždy v pravou chvíli s nabídkou základních hodnot, které většinou není třeba měnit. Kdykoliv však lze zadat nové hodnoty a uložit je na disk. Lze například definovat libovolnou hladinu významnosti, např. 97%, podle níž se provedou všechny testy. Program lze řídit z klávesnice nebo myší.

EDITOR

Pořízení a vstup dat jsou zajištěny datovým editorem, v němž lze data nejen číst z připravených textových souborů a pořizovat, ale rovněž upravovat či zobrazit. Maximální počet dat je 32.000, maximální počet proměnných 255, popř. 3.000. Jsou k dispozici běžné blokové operace, zobrazení dat, ale například i transformace dat podle libovolné funkce. Sloupce, proměnné i libovolné bloky lze pro snazší orientaci pojmenovat.

VÝSTUP

Připravená data se po potvrzení parametrů zpracují zvolenou metodou. Výsledkem výpočtu je textový soubor obsahující vypočtené charakteristiky s vysvětlujícími komentáři. Informace jsou pro větší přehlednost uspořádány do odstavců. Výsledný soubor je v kódu Kamenických a lze jej bez úprav přečíst, a vytisknout kterýmkoliv textovým editorem (i T602). Části výsledků je pak možno použít jako vstupní data k další analýze. Generované grafy lze vytisknout v libovolné velikosti na maticové nebo laserové tiskárně nebo uložit do souboru TIFF a použít později například jako ilustraci zprávy v textovém editoru.

GRAFIKA

Zvlášť velký důraz je kladen na grafické informace a jejich interpretaci. ADSTAT používá místo populárních koláčových, sloupcových či trojrozměrných spíše střízlivější technické grafy, které obsahují daleko víc důležitých informací o chování dat. Z více než 120 diagnostických grafů lze jistě vybrat takové, která prozradí o datech důležitou informaci. Najednou lze zobrazit až 10 grafů, které lze na obrazovce libovolně uspořádat a pak vytisknout. Myší se dá ovládat křížový kurzor, kterým odečtete přesné souřadnice v grafu. Je k dispozici zoom-out, zoom-in (detail) a další funkce.

HELP

Nápověda se dá vyvolat vždy, když ji potřebujete. To znamená, že po stisknutí F1 se objeví popis situace (včetně odkazů), v níž se právě nacházíte. Navíc je k dispozici abecední seznam hesel. Nápověda popisuje jak ovládání programu, tak i stručné informace o statistických technikách a návody k interpretaci grafů.

DOKUMENTACE

Ve 300-stránkovém manuálu je vše potřebné k úplnému zvládnutí práce s ADSTATem. Kromě uživatelského popisu programu je zde také řada příkladů s interpretacemi výsledků a grafů. Celou pětinu manuálu zabírá abecední rejstřík s téměř 400 pojmů a výrazů včetně slovního vysvětlení, vzorců a podobně. V případě potřeby jsou ve vysvětlivkách odkazy na další hesla.

Pro další studium je k dispozici téměř 1000-stránková monografie M. Meloun, J. Militký: Statistické zpracování experimentálních dat, která slouží jako vysokoškolská učebnice u nás a ve svém anglickém vydání i v zahraničí. Popisuje matematické pozadí metod systému ADSTAT se 399 ilustrativními příklady použití a 269 odkazy na studium další literatury. Tato kniha získala cenu Fondu českého svazu spisovatelů za rok 1991 a koncem roku 1992 vyšla anglicky v nakladatelství Ellis Horwood,

ADSTAT se uplatnil jako prostředek pro statistickou analýzu především ve výzkumných ústavech, podnikových i státních laboratořích a zkušebnách, při kontrole kvality, ale i například v ekonomice a ekonometrii, sociologii, medicíně, biologii, sledování životního prostředí a jiných oborech. Pro svou jednoduchost se používá při výuce absolventů na dvaceti vysokých školách v ČR a SR.

Statistický systém ADSTAT verze 2.0 je určen všem uživatelům osobních počítačů třídy s operačním systémem Windows nebo MS DOS, kteří potřebují ve své práci aplikovat moderní statistické techniky. Kompletní instalace zabírá necelých 9 MB na pevném disku. Z tiskáren jsou podporovány 9- a 24 jehličkové (Epson, IBM) i laserové (PCL-5) tiskárny a dále všechny tiskárny, které umí tyto standardy emulovat.

Moduly ADSTATu

ADSTAT nabízí 8 základních modulů obsahujících více jak 30 statistických metod poskytujících stovky informací o zpracovávaných datech. Práci usnadňuje výkonný tabulkový editor, manažer diskových souborů a dynamický grafický výstup společně s přehledným tabulkovým výstupem. Data, která byla zadána v editoru lze zpracovávat libovolnými moduly. Grafické výstupy lze tisknout v prezentační kvalitě, nebo ukládat do souborů pro snadný export do jiných programových balíků.
    ADSTAT je dodáván jako modulární systém zahrnující vždy základní uživatelské prostředí včetně datového editoru a tabelárního a grafického výstupu dat, které je doplněno o příslušný statistický modul zpracování dat. V plné verzi obdrží uživatel všech 8 modulů.

Přehled modulů
Modul Základní statistika
Odhady parametrů
Dva výběry
Porovnání rozdělení
Pravděpodobnostní modely
Mocninná transformace
Exploratorní analýza
Základní předpoklady
Šíření chyb
Diskrétní rozdělení

Modul obsahuje postupy statistické analýzy jednorozměrných výběrů. Jsou zde zahrnuty postupy průzkumové analýzy dat, (umožňující zkoumání statistických zvláštností, konstrukci funkcí charakterizujících rozdělení výběru, porovnání výběrového rozdělení s teoretickými a mocninnou transformaci dat), resp. postupy konfirmační analýzy (odhady parametrů polohy a rozptýlení, testy shody dvou výběrů). Metoda Pravděpodobnostní modely je určena pro odhady parametrů a statistickou analýzu základních pravděpodobnostních modelů na základě daného výběru. Dále obsahuje metody Základní předpoklady pro ověření normality a dalších předpokladů o datech, Dva výběry pro porovnání průměrů a rozptylů dvou jednorozměrných výběrů, Porovnání rozdělení, Mocninnou transformaci, Šíření chyb pro simulaci a analýzu rozdělení funkce náhodných proměnných a Exploratorní grafy pro diskrétní rozdělení.

Ukázka výstupu z metody Odhady parametrů:
ZÁKLADNĺ STATISTIKA
Analýza jednorozměrného výběru
V Ý S T U P  
   
(1) PARAMETRY TVARU:  
   
Šikmost: 4.1992E-01
Špičatost: 2.4207E+00
   
(2) KLASICKÉ ODHADY PARAMETRŮ (za předpokladu normality):  
   
Průměr: 3.6016E+01
Směr. odchylka: 6.1624E-01
Rozptyl: 3.7975E-01
95.0% spolehlivost:   
Spodní mez: 3.5819E+01
Horní mez: 3.6213E+01
   
(3) OSTATNĺ ODHADY POLOHY:  
   
   
Odhad modu: 3.5956E+01
Odhad polosumy: 3.6223E+01
   
(4) ROBUSTNĺ ODHADY PARAMETRŮ (pro neplatnost normality):  
   
Medián: 3.5936E+01
Směr. odchylka: 7.9134E-01
Rozptyl: 6.2622E-01
Směr. odchylka: 8.3068E-02
Rozptyl (nepar.): 6.9003E-03
Směr. odchylka: 7.9961E-02
Rozptyl (Marritz): 6.3938E-03
95.0% spolehlivost:   
Spodní mez: 3.5774E+01
Horní mez: 3.6097E+01
   
   
Uřezání 5% (pro P=0.05):  
Průměr: 3.5998E+01
Směr. odchylka: 6.4947E-01
Rozptyl: 4.2181E-01
Průměr, winsor.: 3.6013E+01
St.odch. winsor.: 6.0752E-01
Rozptyl, winsor.: 3.6908E-01
95.0% spolehlivost:   
Spodní mez: 3.5789E+01
Horní mez: 3.6206E+01
   
Uřezání 40% (pro P=0.40):  
Průměr: 3.5942E+01
Směr. odchylka: 3.0126E-01
Rozptyl: 9.0759E-02
Průměr, winsor.: 3.5940E+01
St.odch. winsor.: 1.2603E-01
Rozptyl, winsor.: 1.5883E-02
95.0% spolehlivost:   
Spodní mez: 3.5832E+01
Horní mez: 3.6052E+01
   
Biweight:  
Průměr: 3.5992E+01
Směr. odchylka: 6.3401E-01
Rozptyl: 4.0197E-01
Váhy sqrt(w): 6.0683E+00
95.0% spolehlivost:   
Spodní mez: 3.5780E+01
Horní mez: 3.6203E+01
   
(5) ADAPTIVNĺ ODHADY PARAMETRŮ:  
   
Hoogovy odhady:  
Relativní délka konců: 2.3354E+00
Průměr: 3.6016E+01
Směr. odchylka: 6.1624E-01
Rozptyl: 3.7975E-01
95.0% spolehlivost:  
Spodní mez: 3.5819E+01
Horní mez: 3.6213E+01
   
   
Začátek výpočtu: 11:34:29.28
Konec výpočtu: 11:34:29.33

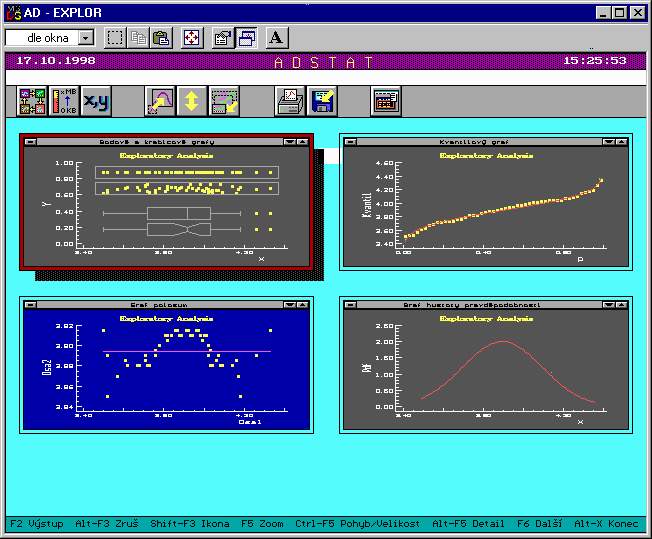
Ukázka vybraných exploratorních grafů modulu Základní statistika

Modul Vícerozměrná data
Kovariance
Korelace
Vícerozměrné výběry
Exploratorní grafy

Tento modul umožňuje analýzu jednoho nebo dvou vícerozměrných výběrů. Obsahuje postupy pro grafické znázornění vícerozměrných dat, odhady parametrů polohy a kovariančních matic včetně souvisejících testů, výpočty různých typů korelačních koeficientů, techniky pro posouzení normality rozdělení a analýzu na hlavních komponentách.

Modul Analýza rozptylu
Anova#1 - jednofaktorová
Anova2P - dvoufaktorová (jedno pozorování)
Anova2B - dvoufaktorová (stejný počet pozorování, vyvážený plán)
Anova2U - dvoufaktorová (nestejný počet pozorování, nevyvážený plán)

Modul je sestaven ze čtyř metod pro analýzu rozptylu (ANOVA) a konstrukci odpovídajících modelů pro případ jednoho, resp. dvou faktorů. Analýza se provádí spíše jako hledání nejvhodnějšího modelu z hlediska regrese s přihlédnutím k různým druhům interakcí. V případě jednoho faktoru se provádí analýza za předpokladu pevných efektů a obecně nevyvážených plánů (různý počet opakování). V případě dvou faktorů lze provádět zpracování vyvážených i nevyvážených plánů a pevných efektů. Provádí se rovněž klasická a robustní dvoufaktorová analýza rozptylu pro případ bez opakování experimentů (v každé cele je jedna hodnota).

Modul Kalibrace
Kalibrační přímka
Lineární spline
Kvadratický spline
Kubický spline

Modul je určen pro konstrukci modelů kalibrační přímky nebo libovolné kalibrační závislosti v laboratořích. U všech modelů se počítají také specifické charakteristiky kalibrace (mez stanovení, mez detekce). V případě kalibrační závislosti libovolného typu se používají speciální regresní modely ve tvaru lineárních, kvadratických, resp. kubických spline. Dostatečná flexibilita je zde zajištěna různou možností volby uzlových bodů. Úkolem kalibrace je také výpočet hodnot kalibrované veličiny podle dané tabulky hodnot odezvy (proměnné y) včetně intervalu spolehlivost pro každý údaj.

Modul Vyhlazování
Reinschův spline
Späthův spline
Savitzky-Golay spline

Tento modul je určen pro vyhlazování experimentálních dat s využitím kubických splinů podle Reinsche, resp. Spätha s výpočtem a analýzou vyhlazeného průběhu, první a druhé derivace, integrálu a nalezení lokálních extrémů a inflexů. Pro digitální filtraci dat se využívá lokální polynomické regrese (Savitzki - Golay).

Modul Lineární regrese

Modul obsahuje postupy pro konstrukci, odhad parametrů a statistickou analýzu libovolných lineárních a linearizovatelných regresních modelů s využitím metody nejmenších čtverců a racionálních hodností. Je možné provádět rozsáhlou regresní diagnostiku, zaměřenou především na kvalitu dat a splnění základních předpokladů metody nejmenších čtverců. Konstrukce parciálních regreseních grafů a dalších 30 diagnostik umožní vizuální posouzení kvality regrese i v případě mnoha nezávisle proměnných. Lze využít možnosti polynomické regrese a její obdoby pro vícerozměrný případ - Taylorova rozvoje do druhého stupně. Metoda racionálních hodností poskytuje na rozdíl od klasické metody nejmenších čtverců mírně vychýlené odhady, které však mají nižší rozptyl. Tato metoda je nepostradatelná v případě multikolinearity, která bývá častým problémem znehodnocujícím celou regresi (např. v polynomické regresi).

Ukázka vstupního panelu:

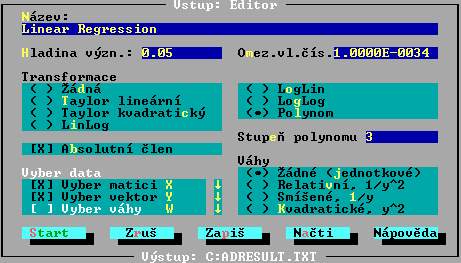
Ukázka panelu pro grafy:

Ukázka výstupu (zkráceno):
Všimněte si rychlosti výpočtu 270ms!
LINEÁRNĺ REGRESE
           
Regresní diagnostika          
Název: Linear Regression          
           
V S T U P          
           
(1) ZVOLENÁ STRATEGIE REGRESNĺ ANALÝZY:
Omezení, P: 1.0000E-34        
Transformace: Polynom        
Stupeň polynomu: 3        
Váhy: Ne        
Absolutní člen zahrnut: Ano        
           
           
(2) PODMĺNKY A KVANTILY PRO STATISTICKÉ TESTY:
Hladina významnosti, alfa: 0.050        
Počet bodů, n: 40        
Počet parametrů, m: 3        
Kvantil Studentova rozdělení t(1-alpha/2,n-m): 2.028         
Kvantil rozd. Chí-kvadrát Chi-square(1-alpha,m): 9.488         
Jméno výstupního souboru: ADRESULT.TXT        
           
           
           
           
V Ý S T U P          
           
(1) PŘEDBĚŽNÁ STATISTICKÁ ANALÝZA:
Proměnná Průměr Směrodatná Párový korelační Spočtená  
    odchylka koeficient hladina výz.  
y 3.5034E+01 6.9138E-01 1.0000 -----  
x1 3.6016E+01 6.1624E-01 0.2290 0.155  
x2 1.2975E+03 4.4548E+01 0.2297 0.154  
x3 4.6759E+04 2.4161E+03 0.2304 0.153  
           
Párové korelační koeficienty mezi dvojicemi Spočtená        
vysvětlujících proměnných hladina významnosti        
x1 versus x2 : 9.9996E-01 0.000      
x1 versus x3 : 9.9982E-01 0.000      
x2 versus x3 : 9.9996E-01 0.000      
           
           
(2) INDIKACE MULTIKOLINEARITY:          
Č Vlastní čísla Čísla podmí- Variance inflation Vícenás.korel.  
[j] korel. matice l[j] něnosti K[j] factor VIF[j] koef pro X[j]  
1 2.0225E-09 1.4832E+09 8.2501E+07 1.0000  
2 1.7650E-04 1.6996E+04 3.2962E+08 1.0000  
3 2.9998E+00 1.0000E+00 8.2329E+07 1.0000  
Maximální číslo podmíněnosti K: 1.4832E+09        
(K[j], K > 1000 indikuje silnou multikolinearitu)          
(VIF[j] > 10 indikuje silnou multikolinearitu)          
           
           
(3) ODHADY PARAMETRŮ A TESTY VÝZNAMNOSTI:
Parametr Odhad Směrodatná Test H0: B[j] = 0 vs. HA: B[j] <> 0    
    odchylka t-kriterium hypoteza H0 je Hlad. výz.
B[ 0] 3.9995E+02 1.9867E+04 2.0132E-02 Akceptována 0.984
B[ 1] -2.6267E+01 1.6483E+03 -1.5936E-02 Akceptována 0.987
B[ 2] 6.0823E-01 4.5574E+01 1.3346E-02 Akceptována 0.989
B[ 3] -4.4498E-03 4.1997E-01 -1.0596E-02 Akceptována 0.992
           
(4) STATISTICKÉ CHARAKTERISTIKY REGRESE:
Vícenásobný korelační koeficient, R: 2.4122E-01        
Koeficient determinace, R^2: 5.8189E-02        
Predikovaný korelační koeficient, Rp^2: 0.0000E+00        
Střední kvadratická chyba predikce, MEP: 5.4259E-01        
Akaikeho informační kritérium, AIC: -2.4936E+01        
           
           
(5) ANALÝZA KLASICKÝCH REZIDUĺ:
           
Bod Meřená Predikovaná Směrodatná Klasické Relativní
  hodnota hodnota odchylka reziduum reziduum
i yexp[i] yvyp[i] s(yvyp[i]) e[i] er[i]
1 3.6181E+01 3.5156E+01 2.1083E-01 1.0255E+00 2.8342E+00
2 3.4929E+01 3.4971E+01 1.5519E-01 -4.1949E-02 -1.2010E-01
3 3.6403E+01 3.5413E+01 2.9786E-01 9.9027E-01 2.7203E+00
4 3.4549E+01 3.4962E+01 1.5808E-01 -4.1314E-01 -1.1958E+00
5 3.3923E+01 3.4898E+01 1.7268E-01 -9.7556E-01 -2.8758E+00
           
Rezidualní součet čtverců, RSC: 1.7557E+01        
Průměr absolutních hodnot reziduí, Me: 5.6414E-01        
Průměr relativních reziduí, Mer: 1.6086E+00        
Odhad reziduálního rozptylu, s^2(e): 4.8771E-01        
Odhad směrodatné odchylky reziduí, s(e): 6.9836E-01        
Odhad šikmosti reziduí, g1(e): 2.4300E-01        
Odhad špičatosti reziduí, g2(e): 1.9752E+00        
           
           
(6) TESTOVÁNĺ REGRESNĺHO TRIPLETU (DATA + MODEL + METODA):
           
Fisher-Snedocorův test významnosti regrese, F: 7.4141E-01        
Tabulkový kvantil, F(1-alpha,m-1,n-m): 2.8663E+00        
Závěr: Navržený model není významný.          
Spočtená hladina významnosti: 0.534        
           
Scottovo kriterium multikolinearity, M: 9.9915E-01        
Závěr: Navržený model není korektní.          
           
Cook-Weisbergův test heteroskedasticity, Sf: 1.8701E-01        
Tabulkový kvantil, Chi^2(1-alpha,1): 3.8415E+00        
Závěr: Rezidua vykazují homoskedasticitu.          
Spočtená hladina významnosti: 0.665        
           
Jarque-Berraův test normality reziduí, L(e): 2.1442E+00        
Tabulkový kvantil, Chi^2(1-alpha,2): 5.9915E+00        
Závěr: Normalita je prokázána.          
Spočtená hladina významnosti: 0.342        
           
Waldův test autokorelace, Wa: 5.5498E+00        
Tabulkový kvantil, Chi^2(1-alpha,1): 3.8415E+00        
Závěr: Rezidua jsou autokorelována.          
Spočtená hladina významnosti: 0.018        
           
Znamékový test, Dt: 1.7620E+00        
Tabulkový kvantil, N(1-alpha/2): 1.6449E+00        
Závěr: Rezidua vykazují trend.          
Spočtená hladina významnosti: 0.039        
           
           
           
(7) INDIKACE VLIVNÝCH BODŮ:
(* indikuje odlehlý nebo vlivný bod)          
           
Bod Standardizované Jackknife Predikované Diagonální  
  reziduum reziduum reziduum prvky  
i eS[i] eJ[i] eP[i] H[i,i]  
1 1.5402E+00 1.5714E+00 1.1283E+00 9.1141E-02   
2 -6.1608E-02 -6.0749E-02 -4.4128E-02 4.9381E-02   
3 1.5677E+00 1.6015E+00 1.2105E+00 1.8192E-01   
           
Bod Zobecněné diag. Cookova Atkinsonova Vliv na  
  prvky vzdálenost vzdálenost predikci  
i Hm[i,i] D[i] A[i] DF[i]  
1 1.5103E-01 5.9475E-02 1.4928E+00 4.9760E-01   
2 4.9481E-02 4.9291E-05 4.1537E-02 -1.3846E-02   
3 2.3777E-01 1.3664E-01 2.2656E+00* 7.5519E-01*   
           
Bod  Věrohodnostní vzdálenosti    
i LD(b)[i]  LD(s^2)[i] LD(b,s^2)[i]    
1 2.6346E-01 3.7256E-02 3.1316E-01    
2 2.1907E-04 1.2607E-02 1.2821E-02    
3 6.0272E-01 4.1850E-02 6.7734E-01    
           
Počátek výpočtu :  11:57:03.63        
Konec výpočtu :  11:57:03.85        

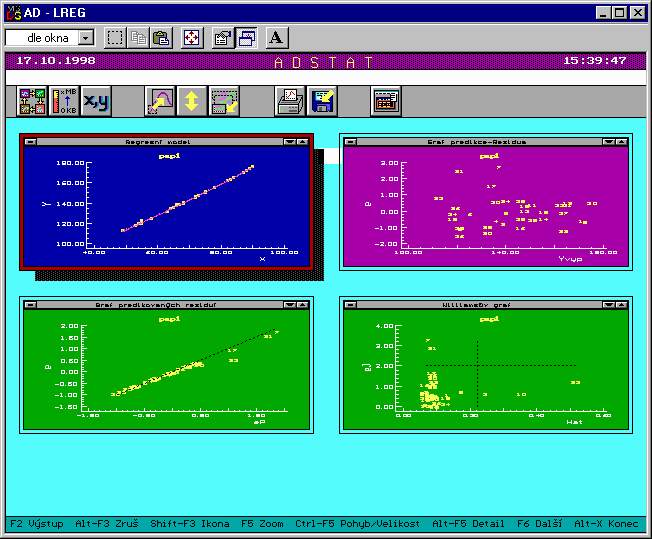
Ukázka vybraných diagnostických grafů modulu Lineární regrese

Modul Nelineární regrese

Modul je určen pro statistickou analýzu a odhad parametrů v nelineárních regresních modelech metodou nejmenších čtverců. Uživatel zadává typ regresního modelu v běžném tvaru algebraickém tvaru. Z používaných funkcí lze vytvořit knihovnu, ze které se pak požadovaná funkce jen vybere. Pro optimalizaci parametrů je použito spolehlivé a efektivní metody MINOPT.

Ukázka vstupního panelu:

Ukázka výstupu (zkráceno):
NELINEÁRNĺ REGRESE
           
Minopt          
Název: Nonlinear Regression          
           
V S T U P          
           
(1) PODMĺNKY:
Hladina významnosti, alfa: 0.050        
Počet bodů, n: 40        
Počet parametrů, m: 3        
Počet nezávislých proměnných: 1        
Minimální změna RSC [%]: 1.000000E-01        
Minimální změna parametrů [%]: 0.000000E+00        
Maximální počet iterací: 150        
Kvantil Studentova rozdělení t(1-alfa/2,n-m): 2.026        
Kvantil Fisher-Snedecorova rozdělení F(1-alfa,n,n-m): 1.694        
Kvantil Chi^2 rozdělení Chi^2(1-alfa,m): 7.815        
Jméno výstupního souboru: ADRESULT        
           
           
(2) REGRESNĺ FUNKCE A POČÁTEČNĺ ODHADY PARAMETRŮ:
Regresní funkce:p[ 1]+p[ 2]*exp(x1*p[ 3])          
p[ 1] :p 1.000000E+00          
p[ 2] :p 1.000000E+00          
p[ 3] :p 1.000000E+00          
           
V Ý S T U P :          
           
           
(1) BODOVÉ ODHADY PARAMETRŮ:
Parametr Bodový Směrodatná Absolutní Relativní  
  odhad odchylka vychýlení vychýlení[%]  
p[ 1] 3.483297E+01 4.612485E-01 -8.586641E-01 -2.465090E+00  
p[ 2] 1.733422E-19 1.397218E-17 5.855298E-16 3.377884E+05  
p[ 3] 1.147780E+00 2.151691E+00 -3.465474E+00 -3.019284E+02  
           
           
(2) INTERVALOVÉ ODHADY PARAMETRŮ:
Parametr Bodový Poloviční délka konfidenčního int. spočtená z:  
  odhad délky poloos maxim    
p[ 1] 3.483297E+01 +- 1.259822E+00 +- 1.350788E+00    
p[ 2] 1.733422E-19 +- 1.504325E-16 +- 4.091817E-17    
p[ 3] 1.147780E+00 +- 6.300574E+00 +- 6.301328E+00    
           
           
(3) KORELAČNĺ MATICE ODHADŮ:
           
  x[1,i] x[2,i] x[3,i]    
x[1,i] 1.0000E+00 -9.2935E-01 9.2697E-01     
x[2,i] -9.2935E-01 1.0000E+00 -9.9997E-01     
x[3,i] 9.2697E-01 -9.9997E-01 1.0000E+00     
         
           
           
(4) STATISTICKÉ CHARAKTERISTIKY REGRESE:
Reziduální součet čtverců, RSC: 1.754350E+01        
Regresní rabat, D^2 [%]: 5.893504E+00        
Akaikeho informační kriterium, AIC: -2.696785E+01        
           
           
(5) ANALÝZA KLASICKÝCH REZIDUĺ:
Bod Meřená Predikovaná Směrodatná Vychýlení Klasické
  hodnota hodnota odchylka   reziduum
i yexp[i] yvyp[i] s(yvyp[i]) hy[i] e[i]
1 3.6181E+01 3.5130E+01 1.8444E-01 -2.3162E-02 1.0512E+00
2 3.4929E+01 3.4976E+01 1.2207E-01 4.9797E-02 -4.6561E-02
3 3.6403E+01 3.5417E+01 2.8386E-01 -6.6410E-02 9.8639E-01
4 3.4549E+01 3.4968E+01 1.2083E-01 4.8414E-02 -4.1978E-01
5 3.3923E+01 3.4912E+01 1.5858E-01 -1.0898E-02 -9.8953E-01
6 3.6265E+01 3.4898E+01 1.8529E-01 -4.8721E-02 1.3664E+00
           
Reziduální součet čtverců, RSC: 1.7543E+01        
Průměr absolutních hodnot reziduí, MA: 5.6231E-01        
Průměr relativních hodnot reziduí, MR: 1.6057E+00        
Odhad reziduálního rozptylu, s^2(e): 4.7415E-01        
Odhad reziduální směrodatná odchylky, s(e): 6.8858E-01        
Odhad šikmosti reziduí, g1(e): -5.9639E-03        
Odhad špičatosti reziduí, g2(e): 4.9484E-02        
Střední kvadratická chyba predikce: 5.0492E-01        
           
           
           
(6) INDIKACE VLIVNÝCH BODŮ:
Bod Jackknife Cookova Diagonální Normalizovaná Věrohodnostní
  reziduum vzdálenost prvky vzdálenost vzdálenost
i eJ[i] D[i] H[i,i] FDA LDA
1 1.6189E+00 6.4686E-02 7.1743E-02 1.2432E+22 3.2252E+02
2 -6.7777E-02 5.1056E-05 3.1427E-02 2.1488E-03 3.6578E-03
3 1.6055E+00 1.6871E-01 1.6994E-01 1.9712E+00 1.0347E+00
4 -6.1401E-01 4.0606E-03 3.0790E-02 5.7914E-01 3.1250E-01
5 -1.5016E+00 4.0714E-02 5.3038E-02 3.5130E+13 1.9125E+02
6 2.1601E+00 1.1046E-01 7.2405E-02 5.3012E+00 2.4151E+00
           
           
(7) MAPA CITLIVOSTNĺ FUNKCE:
Parametr Relativní Souhrná Relativní    
  změna citlivost změna    
  CjR(-5%) Cj CjR(+5%)    
  [%]   [%]    
p[ 1] 6.4417E-09 1.0000E+00 -5.8280E-09    
p[ 2] -9.8544E+01 2.2425E+36 6.7918E+03    
p[ 3] -9.8688E+01 9.1591E+01 7.5106E+03    
           
Počátek výpočtu :  12:01:11.67        
Konec výpočtu :  12:01:16.56

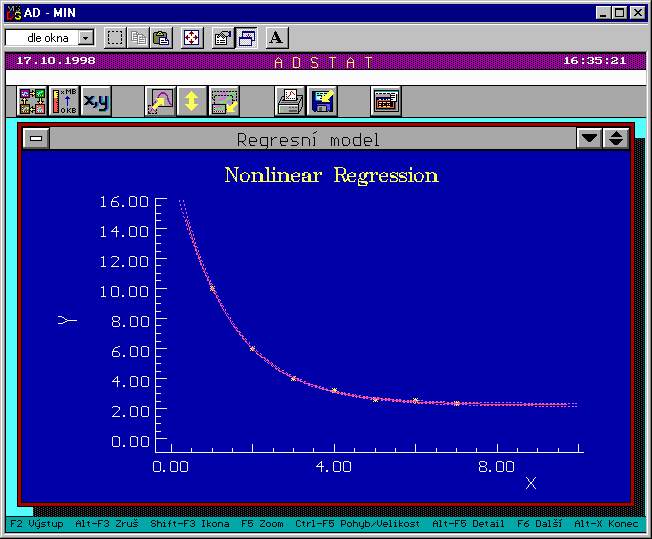
Ukázka proložení regresního modelu v modulu Nelineární regrese

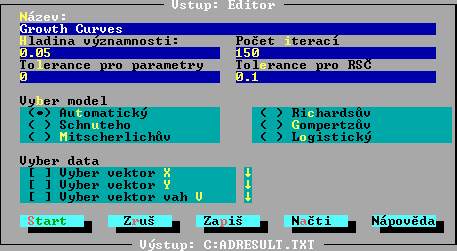
Modul Růstové křivky

Modul umožňuje odhad parametrů a statistickou analýzu základních modelů růstových křivek metodou nelineární regrese. Obsahuje Richardsův, Mitscherlichův, Gompertzův, logistický a Schnutteho model. Pro případ nejistoty o teoretickém typu růstové křivky je nabídnuta také možnost automatické detekce nejvhodnější růstové křivky popisující zadaná data a následný odhad jejich parametrů.

Ukázka vstupního panelu:

TriloByte nabízí dvoudenní semináře na téma použití PC pro statistické zpracování dat přímo na Vašem pracovišti. Forma semináře se přizpůsobuje Vašim potřebám a požadavkům. Ve spolupráci s VŠCHT Pardubice se pořádají týdenní intenzivní nebo dvouleté postgraduální kurzy aplikace statistické analýzy pomocí osobních počítačů se zaměřením na ADSTAT.

Kontaktní adresa:

TriloByte Statistical Software, s.r.o.
U sokolovny 21, 530 02 Pardubice, Czech Republic
tel/fax +420 (0)40-6530891, fax: +420 (0)40-6530892
e-mail: info@trilobyte.anet.cz